Before we proceed further, we will take a short detour to learn about numbers. Internally, computers boil down to machines that move numbers, operate on numbers, read numbers. Numbers. Numbers. NUMBERS!

Let's learn more about how these chunks of metal we call computers, are somehow able to use electricity to represent numbers. Most computers are filled with these tiny components called transistors, which can act as a sort of switch for electric currents. When a small electric current is applied to this transistor "switch", it allows current to flow in another part of the transistor. Therefore, this small electric current determines whether current can flow (1) and current cannot flow (0).

With a large number of transistors, we can create a large array of switches that could be set to the 1 or 0 state.

Let's see how we can represent numbers just using 1s and 0s!

Base-n representation

For most of us, we would have to count with numbers like 1, 2, 3 .. 8, 9, 10. This numbering system is called the base-10 number system, also known as decimal.

We call it base-10 because the number system consists of 10 basic digits.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

By using these 10 digits in an ingenious manner, we humans have been able to represent numbers far beyond our imagination, with only 10 little symbols. Amazing isn't it.

Since we only have 10 digits, we are taught to place these digits side by side in order to represent larger numbers.

For instance, 1234 uses 4 symbols to represent a number far beyond 10. While we intuitively understand that this is one-thousand two-hundred and thirty four, how is this decoded generally?

As we can observe, just the digits alone can only represent 10 values, 0 to 9 (max). In order to go to the next higher value, we use what we commonly refer to as the "tens" place. We place a digit at the position second from the right and we decide that the value of the digit at that spot should be multiplied by 10 to represent its true value. The same is done for the hundreds, thousands, etc.

In general, this is how we can think about this numbering system.

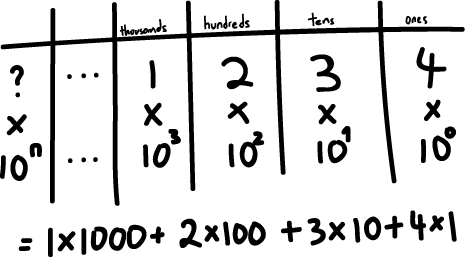
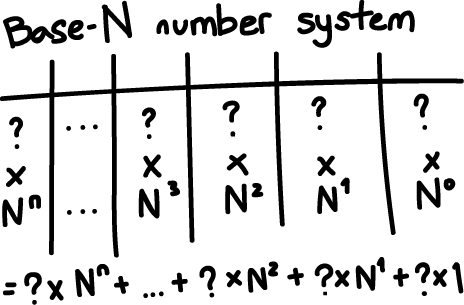
As we see, each digit to the right is multiplied by an increasing power of the base, which in our case is 10.

We can thus generalise this number system to support any possible base N.

Base-2 (Binary)

So let's try to apply what we've learnt to computers!

As I've mentioned earlier, the computer is great at representing 1s and 0s using electric signals.

0, 1

We can observe that we only have 2 "digits" at our disposal. This implies that we should be using the base-2 numbering system!

Referring to our earlier diagram, we know that each digit of a base-2 numbering system will thus have to represent the 2^n place. Thus the first few digits will represent: 1, 2, 4, 8, 16 ... .

So let's try to represent some numbers. The notation we will use will be ??? (n) where n represents the base system we are using.

Let's try to represent the first 5 numbers

0, 1, 2, 3, 4 (10)

Will be:

0, 1, 10, 11, 100 (2)

We can take a look at 11 (2) to understand what's going on. We know that the right-most digit will be multiplied by 2^0 and then the next will be multiplied by 2^1. So we can calculate:

  1 * 2^1 + 1 * 2^0 
= 1 * 2 + 1 * 1
= 2 + 1
= 3        (10)

It works out!

In the computer, this number would be represented by 2 wires being on, therefore in the (1) state for each of them.

This base-2 number system is commonly referred to as binary, and the digits are referred to as bits. This is where the 64-bit in x86-64 comes from! A 64-bit CPU implies that generally, most calculations are done in the CPU utilising 64-bits. Thus while a number like 3 (10) == 11 (2) only requires 2 bits to be represented, the CPU would likely "waste" some bits and use 64-bits to represent the number like so:

0000000000000000000000000000000000000000000000000000000000000011

Base-16 (Hexadecimal)

Another popular numbering system that you would encounter would be hexadecimal. Hexadecimal is a base-16 numbering system. Thus it can represent larger numbers than decimal (base-10) with a smaller amount of hexadecimal digits.

But now you may be wondering, if decimal uses 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 as its 10 digits, how do we have enough symbols for 16 digits? For hexadecimal, they use alphabets to fill up the remaining 6 symbols required.

So the hexadecimal numbering system would make use of:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f

The same general rules apply to this numbering system, and we've left it as an exercise for you to try to understand this numbering system more clearly.

To give you some help, here are some conversions!

Base-10 (decimal)
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

==

Base-16 (hexadecimal)
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f

Base-10 (decimal)
20, 40, 60

==

Base-16 (hexadecimal)
14, 28, 3c

Writing convention

Given that it can be confusing as to what numbering system is being used, there is a conventional way of writing binary, decimal and hexadecimal numbers to prevent ambiguity.

Binary numbers are preprended with 0b. So 0b111 would be a binary number 111.

Hexadecimal numbers are preprended with 0x. So 0x6a would be a hexadecimal number 6a.

If there is no prefix, then the number is assumed to be in decimal. 123 is just 123 in decimal.

Negative numbers

So far, we've only covered non-negative integers (0 ... N). How can we represent negative numbers in the CPU? And more specifically, representing negative numbers in binary.

A logical first idea would be to allocate a single bit for every number, that indicates whether the number is negative or not. A 1 in the is_negative bit indicates the number is negative, while a 0 indicates it is positive.

And this would work very well in fact! However, CPU developers and other computer scientists found a preferable alternative to represent negative numbers which is more suitable for computers.

This method is named 2s-complement.

I will first describe the method, which may sound unintuitive at first. There are 2 steps to convert a positive number to its negative equivalent. We can take the number 5 for instance. Let's consider an imaginary CPU that represents numbers with 4 bits (as compared to 64-bits like our usual CPUs). In such a CPU, the number 5 would look like so:

0101

Now let's go through the steps of 2s complement that will turn it into the representation for -5.

1. Invert all bits of the number (1 -> 0, 0 -> 1)

1010

2. Add 1

  1010
+ 0001
     =
  1011

Now 0b1011 is the binary representation of -5 in our 4-bit system. This may look funny at first, since we understand 0b1011 should represent 11 (decimal) in binary.

But let's see if this 1011 value can fulfill the properties of a negative number. First, we can try to perform addition of -5 with 5.

  1011 (-5)
+ 0101 ( 5)
     =
 10000
     =
  0000 ( 0)

Since our final result has 5-bits, we have to truncate the last bit as we are using a 4-bit representation of numbers for our example. After the truncation, we can see that our result is 0! This works out mathematically, -5 + 5 = 0.

We can even try this with other additions, and it will always work out after truncation!

So how does this work? You may have some clue that the truncation has a big importance to play. This truncation is commonly referred to as an integer overflow, where the result of an operation is larger than the capacity defined for the integer. Thus the extra bits have to be removed, which could lead to inaccuracy.

Somehow, we were able to abuse this behaviour through 2s complement. Let's take a deeper look.

One way to think about integer overflows is a clock. If we imagine that our 4-bit number were stored on a clock, the clock would look like so:

Currently, the clock is pointing at the number 5. Each time we increment the number, the clock hand will move one-step clockwise. If we increment the number too much, it's value will drop back to 0 and start incrementing from there.

Now if we wish to subtract from the number, we could rotate the clock-hand counter-clockwise that many steps.

What if we wanted to avoid doing counter-clockwise rotations? We instead have to rotate the hand clockwise a complement amount of times. If we were to subtract 5 from 5, we know we should end up at 0 in the end.

Try to trace the clock to see how many clockwise steps are required to move the clock hand to 0.

That's right, 11! This is the same value we calculated when we performed the 2s complement calculation earlier :O Thus, the 2s complement method is just a series of steps that allow us to perform this calculation that we did visually, in order to get negative numbers.

By using 2s complement representation to represent negative numbers, we can therefore implement subtraction and addition by only implementing addition. This is a great benefit for CPU developers as they can focus on developing addition for their CPUs without worrying too much about how subtraction can be done. Any subtractions can then be done by first converting the subtracting term using 2s complement, and then performing a simple addition with overflow!

but what about 11?

At this point, we've established how we can represent -5 using 4-bits, but we represented -5 by using the value 11. How would we know whether a number is 11 or -5?

The key to this is that it depends entirely on the context. If we choose to only perform unsigned operations, then we do not care that the 4-bit binary value 1011 could represent -5, we just treat it as 11.

If we chose to perform signed operations, then we treat the value as -5 instead of 11.

Thus during 4-bit unsigned operations, we can use 4-bits to represent the following range of numbers:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ,13, 14, 15

If we needed to make use of negative numbers, then we have to sacrifice some of the positive range in order to represent negative numbers within the same bit-space.

-8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7

In CPUs

Now that we understand how negative numbers could be represented, we just need to extend the size of our integer storage to 32-bits or 64-bits or N-bits according to our CPU. And this is how modern computers represent numbers!